Contents

Logistic Regression

Logistic Regression

Environment setup

import platform

print(f"Python version: {platform.python_version()}")
assert platform.python_version_tuple() >= ("3", "6")

import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
import seaborn as sns

Python version: 3.7.11

D:\ProgramData\Anaconda3\lib\site-packages\pandas\compat\_optional.py:138: UserWarning: Pandas requires version '2.7.0' or newer of 'numexpr' (version '2.6.9' currently installed).
  warnings.warn(msg, UserWarning)

# Setup plots
%matplotlib inline
plt.rcParams["figure.figsize"] = 10, 8
%config InlineBackend.figure_format = 'retina'
sns.set()

import sklearn

print(f"scikit-learn version: {sklearn.__version__}")
assert sklearn.__version__ >= "0.20"

from sklearn.datasets import make_classification, make_blobs
from sklearn.linear_model import SGDClassifier, LogisticRegression
from sklearn.metrics import classification_report

scikit-learn version: 0.20.3

def plot_data(x, y):
    """Plot some 2D data"""

    fig, ax = plt.subplots()
    scatter = ax.scatter(x[:, 0], x[:, 1], c=y, s=40, cmap=plt.cm.RdYlBu)
    legend1 = ax.legend(*scatter.legend_elements(),
                    loc="lower right", title="Classes")
    ax.add_artist(legend1)
    plt.xlim((min(x[:, 0]) - 0.1, max(x[:, 0]) + 0.1))
    plt.ylim((min(x[:, 1]) - 0.1, max(x[:, 1]) + 0.1))


def plot_decision_boundary(pred_func, x, y, figure=None):
    """Plot a decision boundary"""

    if figure is None:  # If no figure is given, create a new one
        plt.figure()
    # Set min and max values and give it some padding
    x_min, x_max = x[:, 0].min() - 0.5, x[:, 0].max() + 0.5
    y_min, y_max = x[:, 1].min() - 0.5, x[:, 1].max() + 0.5
    h = 0.01
    # Generate a grid of points with distance h between them
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    # Predict the function value for the whole grid
    Z = pred_func(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    # Plot the contour and training examples
    plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
    cm_bright = ListedColormap(["#FF0000", "#00FF00", "#0000FF"])
    plt.scatter(x[:, 0], x[:, 1], c=y, s=40, cmap=plt.cm.RdYlBu, alpha=0.8)

Binary classification

Problem formulation

Logistic regression is a classification algorithm used to estimate the probability that a data sample belongs to a particular class.

A logistic regression model computes a weighted sum of the input features (plus a bias term), then applies the logistic function to this sum in order to output a probability.

\[y' = \mathcal{h}_\theta(\pmb{x}) = \sigma(\pmb{\theta}^T\pmb{x})\]

The function output is thresholded to form the model’s prediction:

  • \(0\) if \(y' \lt 0.5\)

  • \(1\) if \(y' \geqslant 0.5\)

Loss function: Binary Crossentropy (log loss)

See loss definition for details.

Model training

  • No analytical solution because of the non-linear \(\sigma()\) function: gradient descent is the only option.

  • Since the loss function is convex, GD (with the right hyperparameters) is guaranteed to find the global loss minimum.

  • Different GD optimizers exist: newton-cg, l-bfgs, sag… Stochastic gradient descent is another possibility, efficient for large numbers of samples and features.

\[\begin{split}\nabla_{\theta}\mathcal{L}(\pmb{\theta}) = \begin{pmatrix} \ \frac{\partial}{\partial \theta_0} \mathcal{L}(\boldsymbol{\theta}) \\ \ \frac{\partial}{\partial \theta_1} \mathcal{L}(\boldsymbol{\theta}) \\ \ \vdots \\ \ \frac{\partial}{\partial \theta_n} \mathcal{L}(\boldsymbol{\theta}) \end{pmatrix} = \frac{2}{m}\pmb{X}^T\left(\sigma(\pmb{X}\pmb{\theta}) - \pmb{y}\right)\end{split}\]

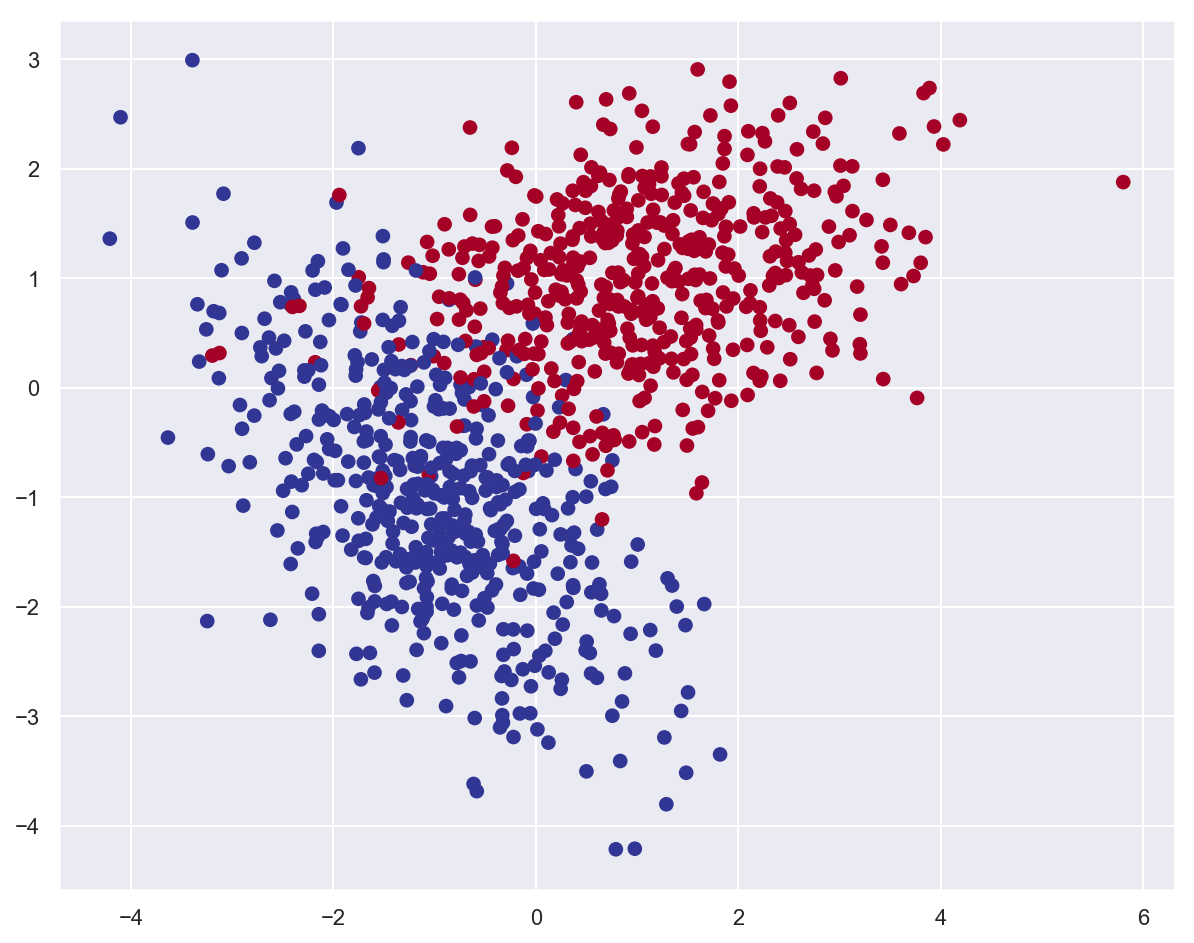
Example: classify planar data

# Generate 2 classes of linearly separable data
x_train, y_train = make_classification(
    n_samples=1000,
    n_features=2,
    n_redundant=0,
    n_informative=2,
    random_state=26,
    n_clusters_per_class=1,
)
plot_data(x_train, y_train)

---------------------------------------------------------------------------
AttributeError                            Traceback (most recent call last)
<ipython-input-5-1b1108a63e4a> in <module>
      8     n_clusters_per_class=1,
      9 )
---> 10 plot_data(x_train, y_train)

<ipython-input-4-b2991d7dc072> in plot_data(x, y)
      4     fig, ax = plt.subplots()
      5     scatter = ax.scatter(x[:, 0], x[:, 1], c=y, s=40, cmap=plt.cm.RdYlBu)
----> 6     legend1 = ax.legend(*scatter.legend_elements(),
      7                     loc="lower right", title="Classes")
      8     ax.add_artist(legend1)

AttributeError: 'PathCollection' object has no attribute 'legend_elements'
_images/logistic_regression_11_1.png 
# Create a Logistic Regression model based on stochastic gradient descent
# Alternative: using the LogisticRegression class which implements many GD optimizers
lr_model = SGDClassifier(loss="log")

# Train the model
lr_model.fit(x_train, y_train)

print(f"Model weights: {lr_model.coef_}, bias: {lr_model.intercept_}")

Model weights: [[-2.96719034 -2.55668143]], bias: [-0.57585284]

# Print report with classification metrics
print(classification_report(y_train, lr_model.predict(x_train)))

              precision    recall  f1-score   support

           0       0.96      0.92      0.94       502
           1       0.92      0.96      0.94       498

    accuracy                           0.94      1000
   macro avg       0.94      0.94      0.94      1000
weighted avg       0.94      0.94      0.94      1000

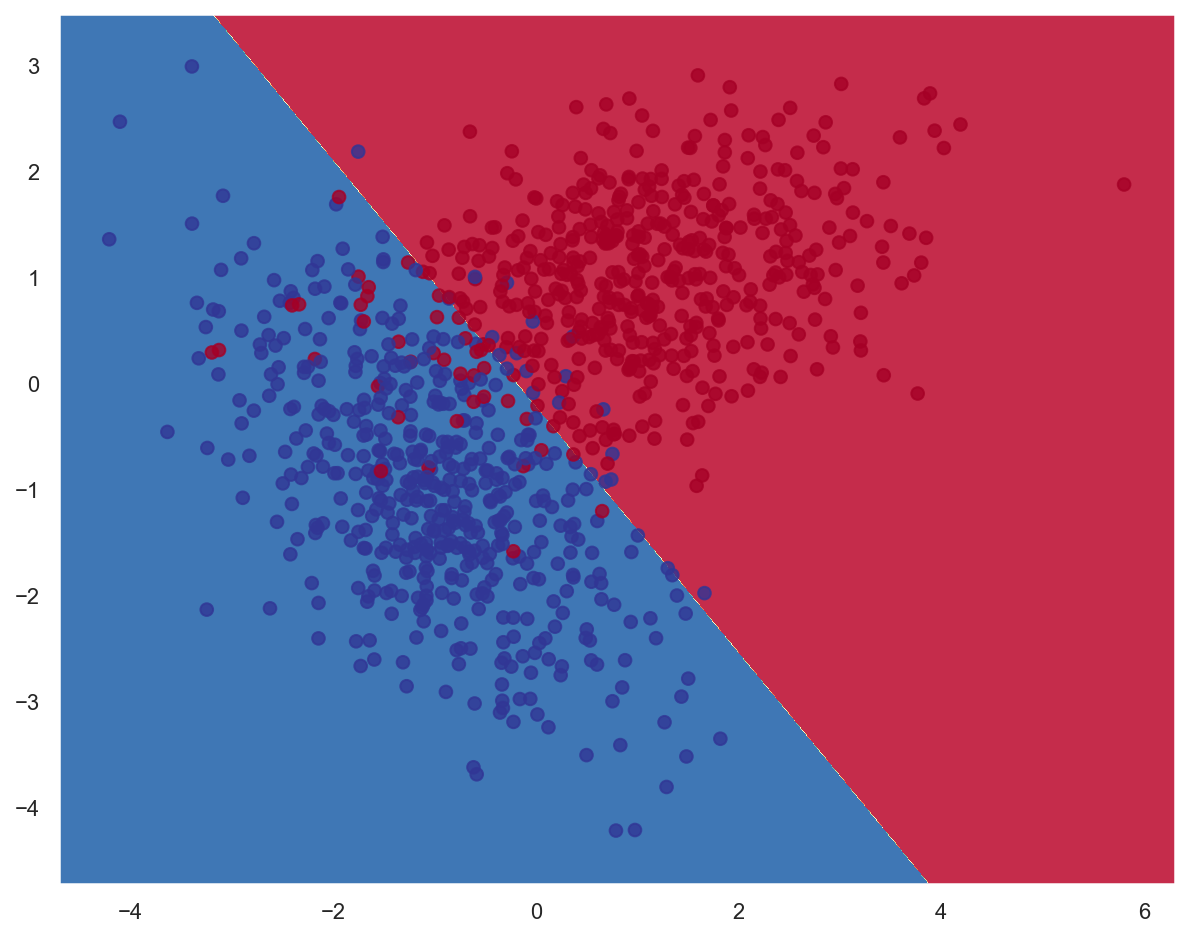
# Plot decision boundary
plot_decision_boundary(lambda x: lr_model.predict(x), x_train, y_train)
_images/logistic_regression_14_0.png

Multivariate regression

Problem formulation

Multivariate regression, also called softmax regression, is a generalization of logistic regression for multiclass classification.

A softmax regression model computes the scores \(s_k(\pmb{x})\) for each class \(k\), then estimates probabilities for each class by applying the softmax function to compute a probability distribution.

For a sample \(\pmb{x}^{(i)}\), the model predicts the class \(k\) that has the highest probability.

\[s_k(\pmb{x}) = {\pmb{\theta}^{(k)}}^T\pmb{x}\]
\[\mathrm{prediction} = \underset{k}{\mathrm{argmax}}\;\sigma(s(\pmb{x}^{(i)}))_k\]

Each class \(k\) has its own parameter vector \(\pmb{\theta}^{(k)}\).

Model output

  • \(\pmb{y}^{(i)}\) (ground truth): binary vector of \(K\) values. \(y^{(i)}_k\) is equal to 1 if the \(i\)th sample’s class corresponds to \(k\), 0 otherwise.

  • \(\pmb{y}'^{(i)}\): probability vector of \(K\) values, computed by the model. \(y'^{(i)}_k\) represents the probability that the \(i\)th sample belongs to class \(k\).

\[\begin{split}\pmb{y}^{(i)} = \begin{pmatrix} \ y^{(i)}_1 \\ \ y^{(i)}_2 \\ \ \vdots \\ \ y^{(i)}_K \end{pmatrix} \in \pmb{R}^K\;\;\;\; \pmb{y}'^{(i)} = \begin{pmatrix} \ y'^{(i)}_1 \\ \ y'^{(i)}_2 \\ \ \vdots \\ \ y'^{(i)}_K \end{pmatrix} = \begin{pmatrix} \ \sigma(s(\pmb{x}^{(i)}))_1 \\ \ \sigma(s(\pmb{x}^{(i)}))_2 \\ \ \vdots \\ \ \sigma(s(\pmb{x}^{(i)}))_K \end{pmatrix} \in \pmb{R}^K\end{split}\]

Loss function: Categorical Crossentropy

See loss definition for details.

Model training

Via gradient descent:

\[\nabla_{\theta^{(k)}}\mathcal{L}(\pmb{\theta}) = \frac{1}{m}\sum_{i=1}^m \left(y'^{(i)}_k - y^{(i)}_k \right)\pmb{x}^{(i)}\]
\[\pmb{\theta}^{(k)}_{next} = \pmb{\theta}^{(k)} - \eta\nabla_{\theta^{(k)}}\mathcal{L}(\pmb{\theta})\]

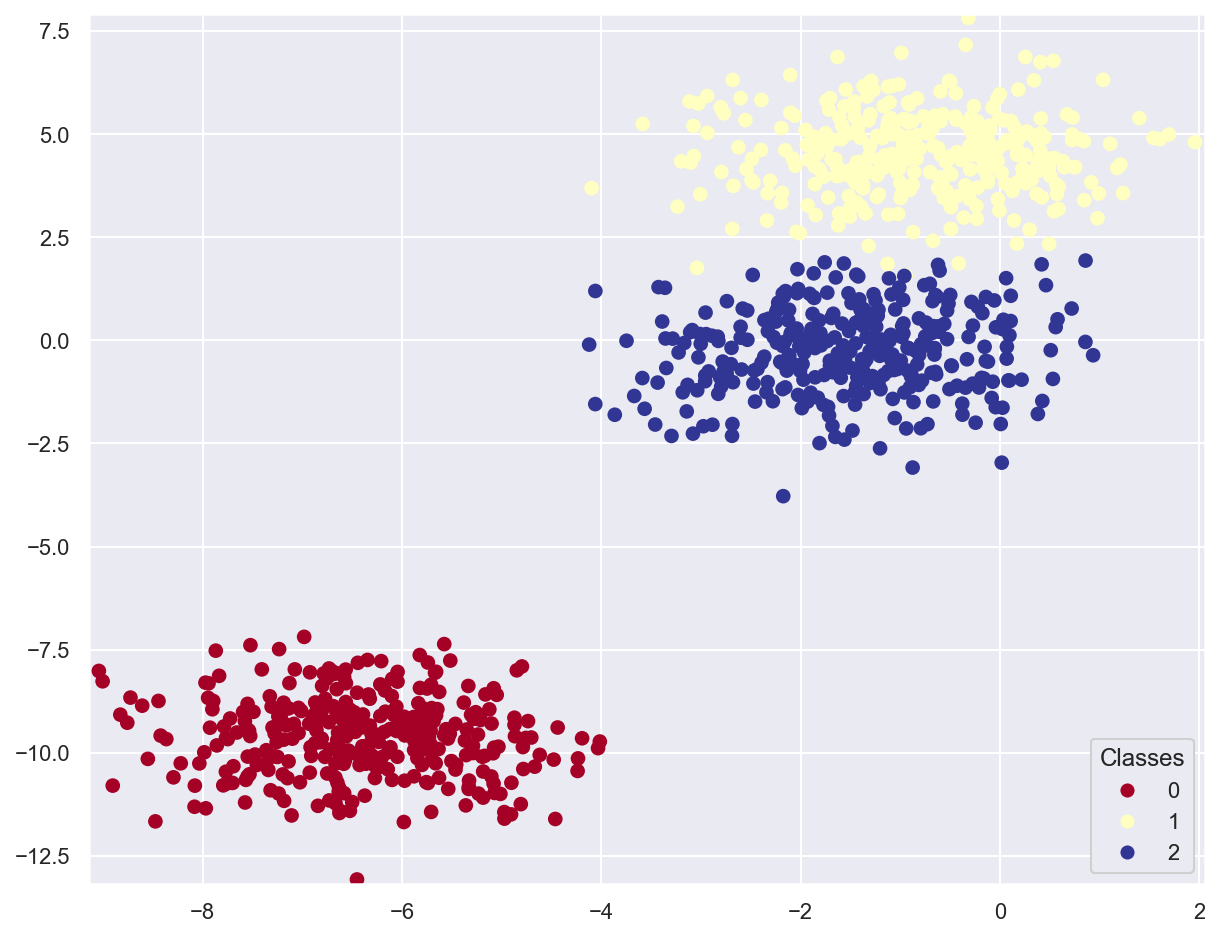
Example: classify multiclass planar data

# Generate 3 classes of linearly separable data
x_train_multi, y_train_multi = make_blobs(n_samples=1000, n_features=2, centers=3, random_state=11)

plot_data(x_train_multi, y_train_multi)
_images/logistic_regression_21_0.png 
# Create a Logistic Regression model based on stochastic gradient descent
# Alternative: using LogisticRegression(multi_class="multinomial") which implements SR
lr_model_multi = SGDClassifier(loss="log")

# Train the model
lr_model_multi.fit(x_train_multi, y_train_multi)

print(f"Model weights: {lr_model_multi.coef_}, bias: {lr_model_multi.intercept_}")

Model weights: [[ -5.76624648 -17.43149458]
 [ -1.27339599  19.17812979]
 [  1.5231193   -0.91647832]], bias: [-133.15588019  -38.36388245    2.53712564]

# Print report with classification metrics
print(classification_report(y_train_multi, lr_model_multi.predict(x_train_multi)))

              precision    recall  f1-score   support

           0       1.00      1.00      1.00       334
           1       0.99      0.99      0.99       333
           2       0.99      0.99      0.99       333

    accuracy                           0.99      1000
   macro avg       0.99      0.99      0.99      1000
weighted avg       1.00      0.99      0.99      1000

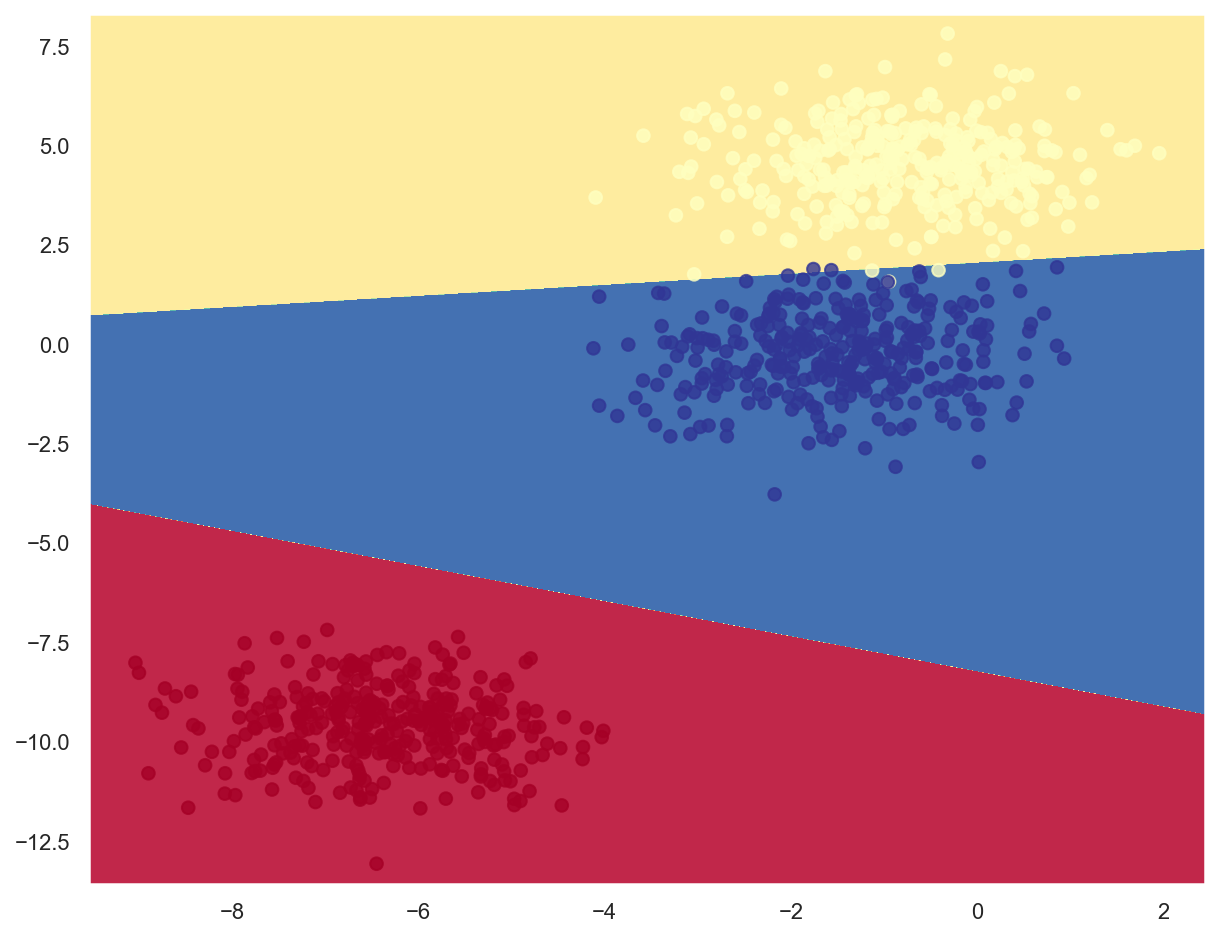
# Plot decision boundaries
plot_decision_boundary(lambda x: lr_model_multi.predict(x), x_train_multi, y_train_multi)
_images/logistic_regression_24_0.png

Titanic Disaster Survival Using Logistic Regression

#import libraries

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

Load the Data

#load data

titanic_data=pd.read_csv('titanic_train.csv')

len(titanic_data)

891

View the data using head function which returns top rows

titanic_data.head()
PassengerId Survived Pclass Name Sex Age SibSp Parch Ticket Fare Cabin Embarked
0 1 0 3 Braund, Mr. Owen Harris male 22.0 1 0 A/5 21171 7.2500 NaN S
1 2 1 1 Cumings, Mrs. John Bradley (Florence Briggs Th... female 38.0 1 0 PC 17599 71.2833 C85 C
2 3 1 3 Heikkinen, Miss. Laina female 26.0 0 0 STON/O2. 3101282 7.9250 NaN S
3 4 1 1 Futrelle, Mrs. Jacques Heath (Lily May Peel) female 35.0 1 0 113803 53.1000 C123 S
4 5 0 3 Allen, Mr. William Henry male 35.0 0 0 373450 8.0500 NaN S 
titanic_data.index

RangeIndex(start=0, stop=891, step=1)

titanic_data.columns

Index(['PassengerId', 'Survived', 'Pclass', 'Name', 'Sex', 'Age', 'SibSp',
       'Parch', 'Ticket', 'Fare', 'Cabin', 'Embarked'],
      dtype='object')

titanic_data.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 891 entries, 0 to 890
Data columns (total 12 columns):
 #   Column       Non-Null Count  Dtype  
---  ------       --------------  -----  
 0   PassengerId  891 non-null    int64  
 1   Survived     891 non-null    int64  
 2   Pclass       891 non-null    int64  
 3   Name         891 non-null    object 
 4   Sex          891 non-null    object 
 5   Age          714 non-null    float64
 6   SibSp        891 non-null    int64  
 7   Parch        891 non-null    int64  
 8   Ticket       891 non-null    object 
 9   Fare         891 non-null    float64
 10  Cabin        204 non-null    object 
 11  Embarked     889 non-null    object 
dtypes: float64(2), int64(5), object(5)
memory usage: 83.7+ KB

titanic_data.dtypes

PassengerId      int64
Survived         int64
Pclass           int64
Name            object
Sex             object
Age            float64
SibSp            int64
Parch            int64
Ticket          object
Fare           float64
Cabin           object
Embarked        object
dtype: object

titanic_data.describe()
PassengerId Survived Pclass Age SibSp Parch Fare
count 891.000000 891.000000 891.000000 714.000000 891.000000 891.000000 891.000000
mean 446.000000 0.383838 2.308642 29.699118 0.523008 0.381594 32.204208
std 257.353842 0.486592 0.836071 14.526497 1.102743 0.806057 49.693429
min 1.000000 0.000000 1.000000 0.420000 0.000000 0.000000 0.000000
25% 223.500000 0.000000 2.000000 20.125000 0.000000 0.000000 7.910400
50% 446.000000 0.000000 3.000000 28.000000 0.000000 0.000000 14.454200
75% 668.500000 1.000000 3.000000 38.000000 1.000000 0.000000 31.000000
max 891.000000 1.000000 3.000000 80.000000 8.000000 6.000000 512.329200

Explaining Dataset

survival : Survival 0 = No, 1 = Yes
pclass : Ticket class 1 = 1st, 2 = 2nd, 3 = 3rd
sex : Sex
Age : Age in years
sibsp : Number of siblings / spouses aboard the Titanic
parch # of parents / children aboard the Titanic
ticket : Ticket number fare Passenger fare cabin Cabin number
embarked : Port of Embarkation C = Cherbourg, Q = Queenstown, S = Southampton

Data Analysis

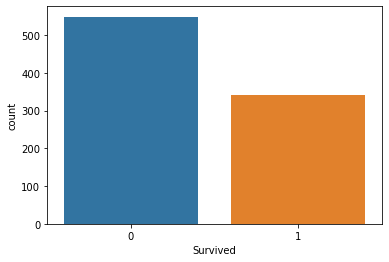
Import Seaborn for visually analysing the data， Find out how many survived vs Died using countplot method of seaboarn

#countplot of subrvived vs not  survived

sns.countplot(x='Survived',data=titanic_data)

<AxesSubplot:xlabel='Survived', ylabel='count'>
_images/logistic_regression_43_1.png

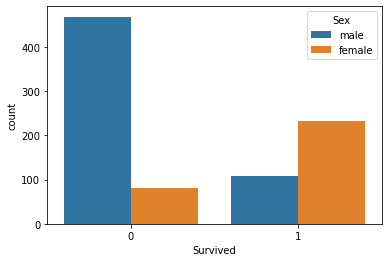
Male vs Female Survival

#Male vs Female Survived?

sns.countplot(x='Survived',data=titanic_data,hue='Sex')

<AxesSubplot:xlabel='Survived', ylabel='count'>
_images/logistic_regression_46_1.png

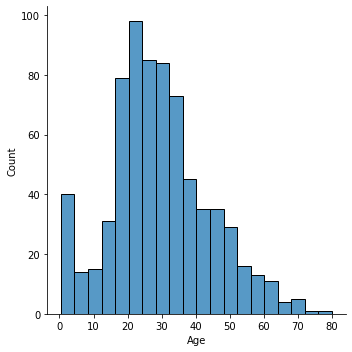
**See age group of passengeres travelled **
Note: We will use displot method to see the histogram. However some records does not have age hence the method will throw an error. In order to avoid that we will use dropna method to eliminate null values from graph

#Check for null

titanic_data.isna()
PassengerId Survived Pclass Name Sex Age SibSp Parch Ticket Fare Cabin Embarked
0 False False False False False False False False False False True False
1 False False False False False False False False False False False False
2 False False False False False False False False False False True False
3 False False False False False False False False False False False False
4 False False False False False False False False False False True False
... ... ... ... ... ... ... ... ... ... ... ... ...
886 False False False False False False False False False False True False
887 False False False False False False False False False False False False
888 False False False False False True False False False False True False
889 False False False False False False False False False False False False
890 False False False False False False False False False False True False

891 rows × 12 columns

#Check how many values are null

titanic_data.isna().sum()

PassengerId      0
Survived         0
Pclass           0
Name             0
Sex              0
Age            177
SibSp            0
Parch            0
Ticket           0
Fare             0
Cabin          687
Embarked         2
dtype: int64

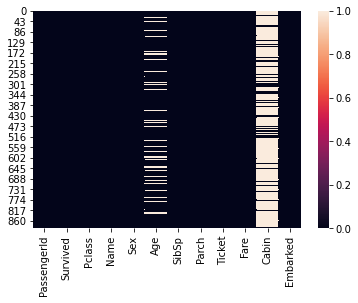
#Visualize null values

sns.heatmap(titanic_data.isna())

<AxesSubplot:>
_images/logistic_regression_53_1.png 
#find the % of null values in age column

(titanic_data['Age'].isna().sum()/len(titanic_data['Age']))*100

19.865319865319865

#find the % of null values in cabin column

(titanic_data['Cabin'].isna().sum()/len(titanic_data['Cabin']))*100

77.10437710437711

#find the distribution for the age column

sns.displot(x='Age',data=titanic_data)

<seaborn.axisgrid.FacetGrid at 0x1509b6c8a30>
_images/logistic_regression_59_1.png

Data Cleaning

Fill the missing values
we will fill the missing values for age. In order to fill missing values we use fillna method.
For now we will fill the missing age by taking average of all age

#fill age column

titanic_data['Age'].fillna(titanic_data['Age'].mean(),inplace=True)

We can verify that no more null data exist
we will examine data by isnull mehtod which will return nothing

#verify null value

titanic_data['Age'].isna().sum()

0

Alternatively we will visualise the null value using heatmap
we will use heatmap method by passing only records which are null.

#visualize null values

sns.heatmap(titanic_data.isna())

<AxesSubplot:>
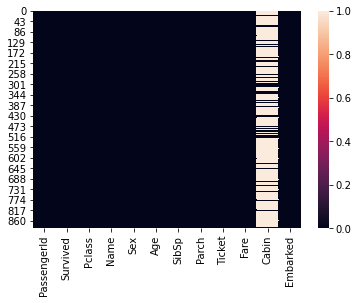
_images/logistic_regression_69_1.png

We can see cabin column has a number of null values, as such we can not use it for prediction. Hence we will drop it

#Drop cabin column

titanic_data.drop('Cabin',axis=1,inplace=True)

#see the contents of the data

titanic_data.head()
PassengerId Survived Pclass Name Sex Age SibSp Parch Ticket Fare Embarked
0 1 0 3 Braund, Mr. Owen Harris male 22.0 1 0 A/5 21171 7.2500 S
1 2 1 1 Cumings, Mrs. John Bradley (Florence Briggs Th... female 38.0 1 0 PC 17599 71.2833 C
2 3 1 3 Heikkinen, Miss. Laina female 26.0 0 0 STON/O2. 3101282 7.9250 S
3 4 1 1 Futrelle, Mrs. Jacques Heath (Lily May Peel) female 35.0 1 0 113803 53.1000 S
4 5 0 3 Allen, Mr. William Henry male 35.0 0 0 373450 8.0500 S

Preaparing Data for Model
No we will require to convert all non-numerical columns to numeric. Please note this is required for feeding data into model. Lets see which columns are non numeric info describe method

#Check for the non-numeric column

titanic_data.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 891 entries, 0 to 890
Data columns (total 11 columns):
 #   Column       Non-Null Count  Dtype  
---  ------       --------------  -----  
 0   PassengerId  891 non-null    int64  
 1   Survived     891 non-null    int64  
 2   Pclass       891 non-null    int64  
 3   Name         891 non-null    object 
 4   Sex          891 non-null    object 
 5   Age          891 non-null    float64
 6   SibSp        891 non-null    int64  
 7   Parch        891 non-null    int64  
 8   Ticket       891 non-null    object 
 9   Fare         891 non-null    float64
 10  Embarked     889 non-null    object 
dtypes: float64(2), int64(5), object(4)
memory usage: 76.7+ KB

titanic_data.dtypes

PassengerId      int64
Survived         int64
Pclass           int64
Name            object
Sex             object
Age            float64
SibSp            int64
Parch            int64
Ticket          object
Fare           float64
Embarked        object
dtype: object

We can see, Name, Sex, Ticket and Embarked are non-numerical.It seems Name,Embarked and Ticket number are not useful for Machine Learning Prediction hence we will eventually drop it. For Now we would convert Sex Column to dummies numerical values****

#convert sex column to numerical values

gender=pd.get_dummies(titanic_data['Sex'],drop_first=True)

titanic_data['Gender']=gender

titanic_data.head()
PassengerId Survived Pclass Name Sex Age SibSp Parch Ticket Fare Embarked Gender
0 1 0 3 Braund, Mr. Owen Harris male 22.0 1 0 A/5 21171 7.2500 S 1
1 2 1 1 Cumings, Mrs. John Bradley (Florence Briggs Th... female 38.0 1 0 PC 17599 71.2833 C 0
2 3 1 3 Heikkinen, Miss. Laina female 26.0 0 0 STON/O2. 3101282 7.9250 S 0
3 4 1 1 Futrelle, Mrs. Jacques Heath (Lily May Peel) female 35.0 1 0 113803 53.1000 S 0
4 5 0 3 Allen, Mr. William Henry male 35.0 0 0 373450 8.0500 S 1 
#drop the columns which are not required

titanic_data.drop(['Name','Sex','Ticket','Embarked'],axis=1,inplace=True)

titanic_data.head()
PassengerId Survived Pclass Age SibSp Parch Fare Gender
0 1 0 3 22.0 1 0 7.2500 1
1 2 1 1 38.0 1 0 71.2833 0
2 3 1 3 26.0 0 0 7.9250 0
3 4 1 1 35.0 1 0 53.1000 0
4 5 0 3 35.0 0 0 8.0500 1 
#Seperate Dependent and Independent variables

x=titanic_data[['PassengerId','Pclass','Age','SibSp','Parch','Fare','Gender']]
y=titanic_data['Survived']

y

0      0
1      1
2      1
3      1
4      0
      ..
886    0
887    1
888    0
889    1
890    0
Name: Survived, Length: 891, dtype: int64

Data Modelling

Building Model using Logestic Regression

Build the model

#import train test split method

from sklearn.model_selection import train_test_split

#train test split

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.33, random_state=42)

#import Logistic  Regression

from sklearn.linear_model import LogisticRegression

#Fit  Logistic Regression 

lr=LogisticRegression()

lr.fit(x_train,y_train)

C:\Users\gggg\anaconda3\lib\site-packages\sklearn\linear_model\_logistic.py:762: ConvergenceWarning: lbfgs failed to converge (status=1):
STOP: TOTAL NO. of ITERATIONS REACHED LIMIT.

Increase the number of iterations (max_iter) or scale the data as shown in:
    https://scikit-learn.org/stable/modules/preprocessing.html
Please also refer to the documentation for alternative solver options:
    https://scikit-learn.org/stable/modules/linear_model.html#logistic-regression
  n_iter_i = _check_optimize_result(

LogisticRegression()

#predict

predict=lr.predict(x_test)

Testing

See how our model is performing

#print confusion matrix 

from sklearn.metrics import confusion_matrix

pd.DataFrame(confusion_matrix(y_test,predict),columns=['Predicted No','Predicted Yes'],index=['Actual No','Actual Yes'])
Predicted No Predicted Yes
Actual No 151 24
Actual Yes 37 83 
#import classification report

from sklearn.metrics import classification_report

print(classification_report(y_test,predict))

              precision    recall  f1-score   support

           0       0.80      0.86      0.83       175
           1       0.78      0.69      0.73       120

    accuracy                           0.79       295
   macro avg       0.79      0.78      0.78       295
weighted avg       0.79      0.79      0.79       295

Precision is fine considering Model Selected and Available Data. Accuracy can be increased by further using more features (which we dropped earlier) and/or by using other model

Note:
Precision : Precision is the ratio of correctly predicted positive observations to the total predicted positive observations
Recall : Recall is the ratio of correctly predicted positive observations to the all observations in actual class F1 score - F1 Score is the weighted average of Precision and Recall.